HPO with Genetic Algorithm

hpo-with-genetic-algorithm

메타휴리스틱(Metaheuristic)

무작위화(randomization)와 전역 탐색(global exploration)을 사용하는 모든 확률적 알고리즘을 지칭.
무작위성을 통해 지역 최적해(local search)의 함정에서 벗어나 전역적인 탐색을 가능하게 함.
비선형 모델링 및 전역 최적화에 적합.

수용 가능한 시간 내에 ‘좋은’ 실행 가능한 해(feasible solution)를 찾는 것이 목표이지만 최적의 해를 찾는다는 보장은 없음.

수학적으로 증명된 길을 따라가는 게 아니라, 여러 번의 시도를 통해 경험적으로 좋은 해를 찾아가는 전략

주요 구성 요소

강화 (Intensification / Exploitation):

현재 찾은 좋은 해(solution)가 있는 지역 주변을 집중적으로 탐색하는 것.
가장 좋은 것을 선택함으로써 최적점에 수렴하려는 전략.

다양화 (Diversification / Exploration):

다양한 해를 생성하여 탐색 공간을 전역적으로 탐험하는 것.
지역 최적해에 갇히는 것을 피하고, 해의 다양성을 높이는 전략.

둘의 균형이 중요. 강화에만 집중하면 지역 최적해에 갇힐 수 있고, 다양화에만 집중하면 수렴 속도가 느려질 수 있음.

대표적인 메타휴리스틱 알고리즘

Population-based:

여러 개의 해(개체)를 하나의 집단으로 만들어 동시에 탐색하고 진화시키는 방법.
Genetic Algorithm (GA), Particle Swarm Optimization (PSO)

Trajectory-based:

하나의 해에서 시작하여 점진적으로 해를 개선해 나가는 방법.
Simulated Annealing (SA)

유전 알고리즘 (Genetic Algorithm, GA)

유전학과 자연선택의 원리에 기반한 강력한 최적화 방법으로 다음과 같은 장점을 가짐:

Gradient-free: 목적 함수가 복잡하거나, 미분 불가능해도 사용할 수 있어 유연성이 높음.
병렬화 용이: 여러 해를 동시에 평가할 수 있어 구현 시 병렬 처리에 유리함.
다양한 파라미터 동시 처리: 여러 파라미터와 그룹을 동시에 조작할 수 있음.

그러나 다음과 같은 단점도 존재:

적합도 함수(fitness function) 공식화: 무엇이 ‘좋은 해’인지를 정의하는 함수를 만드는 것이 어려울 수 있음.
집단 크기(population size) 사용: 집단의 크기를 얼마로 할지 정해야 함.
중요 파라미터 선택: 교차, 변이 확률 등 GA 자체의 여러 파라미터를 잘 선택해야 함.
새로운 집단 선택 기준: 다음 세대를 어떻게 구성할지 기준을 정해야 함.

핵심 개념

염색체 (Chromosome): 여러 유전자(Gene)의 집합. GA에서는 하나의 해(solution) 를 의미.
유전자 (Gene): 염색체를 구성하는 요소. 정보의 한 단위.
집단 (Population): 여러 개의 염색체(해)로 구성된 그룹.
자손 (Offspring): 기존 염색체(부모 해)로부터 생성된 새로운 염색체(새로운 해). 부모의 유전 정보를 물려받음.
적합도 (Fitness): 특정 염색체(해)가 주어진 문제를 얼마나 잘 해결하는지를 나타내는 품질 점수.

GA의 동작 흐름

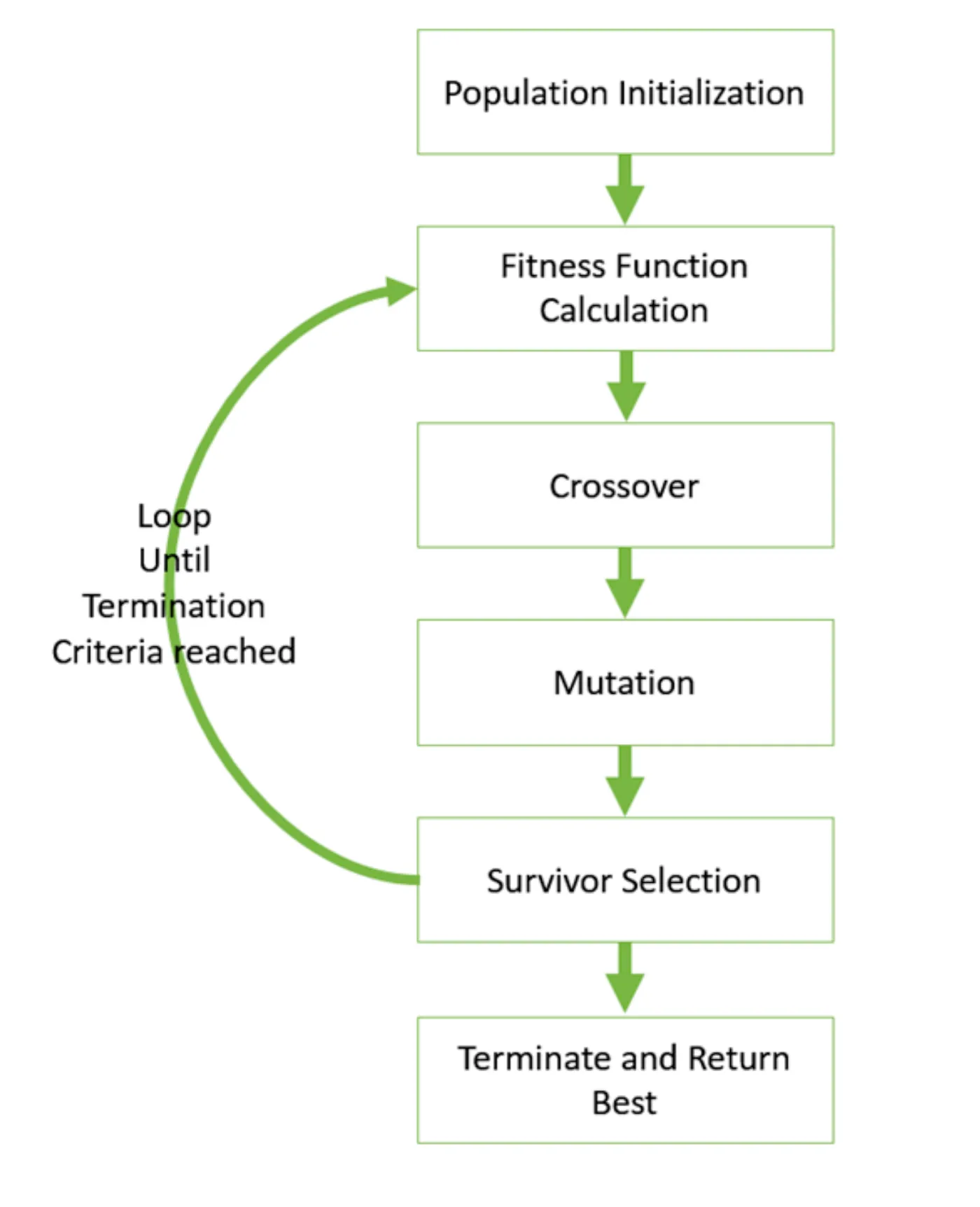
GA Flow

초기 집단 생성 (Population Initialization): 무작위로 여러 개의 해(염색체)를 생성.
적합도 함수 계산 (Fitness Function Calculation): 각 해가 얼마나 좋은지 점수를 매김.
선택, 교차, 변이의 반복 루프: 종료 조건이 만족될 때까지 다음을 반복.
- 교차 (Crossover): 점수가 높은 부모 해들을 선택하여 그들의 유전 정보(파라미터 값)를 섞어 새로운 자식 해를 만듦.
- 돌연변이 (Mutation): 자식 해의 유전 정보를 아주 약간 무작위로 변경하여 다양성을 부여.
- 생존자 선택 (Survivor Selection): 새로운 세대를 구성할 해들(기존 부모 세대 + 자식 세대)을 선택합니다. 보통 적합도가 높은 해들이 살아남음.
종료 및 최적해 반환 (Terminate and Return Best): 반복이 끝나면, 지금까지 찾은 해 중에서 가장 적합도가 높았던 최적의 해를 반환.

HPO with GA (Ridge Regression의 λ 최적화)

문제 정의:

검증 데이터셋(D_val)에 대한 손실 l을 최소화하는 하이퍼파라미터 $\lambda$ 를 찾는 것이 목표.
$0 \leq \lambda \leq 1$ 범위에서 탐색.

데이터 생성 가정:

실제 함수는 y = 2x + 1이라고 가정.
x값 100개를 무작위로 생성하고, y값은 2x + 1에 정규분포 노이즈를 추가하여 생성.
손실 함수: ridge 의 loss $\sum (y - \hat{y})^2 + \lambda * m^2, \quad \text{where } \hat{y} = mx + b$

Example (HPO of Ridge Regression with GA)

import relevant packages

1
import numpy as np
2
from sklearn.linear_model import Ridge
3
from sklearn.model_selection import train_test_split
4
import random

generate data

1
x = np.random.rand(100)
2
y = 2 * x + 1 + np.random.normal(0, 0.1, size=x.shape)

split data into train and validation sets

1
x_train, x_val, y_train, y_val = train_test_split(x, y, train_size=0.8)

lower level optimization problem

1
def lower_opt(x_train, y_train, lambda_val):
2
    model = Ridge(alpha=lambda_val)
3
    model.fit(x_train, y_train)
4
    m = model.coef_
5
    b = model.intercept_
6
    return m, b

upper level evalutaion

1
def upper_eval(x_val, y_val, m, b, lambda_val):
2
    obj = sum((y_val[i] - (m * x_val[i] + b))**2 for i in range(len(y_val))) + lambda_val * m**2
3
    obj = obj[0] # because sum returns a list
4
    return obj

GA for HPO

1
def ga_HPO(x_train, y_train, x_val, y_val, population_size = 10, generation = 50, crossover_rate = 0.8, mutation_rate = 0.1):
2
    # initialize population for a given # of n,
3
    population = [random.uniform(0, 1) for _ in range(population_size)]
4

5
    # generation
6
    for generation in range(generations):
7
        # evaluate fitness
8
        fitness = []
9
        for lambda_val in population:
10
            m, b = lower_opt(x_train, y_train, lambda_val)
11
            eval_fit = upper_eval(x_val, y_val, m, b, lambda_val)
12
            fitness.append(eval_fit)
13

14
        # select parents (sorting by fitness)
15
        selected_population = [population[i] for i in np.argsort(fitness)[:population_size // 2]] # select top 50%
16

17
        # cross over and mutation to create new population
18
        new_population = selected_population.copy()
19
        while len(new_population) < population_size:
20
            # crossover
21
            if random.random() < crossover_rate:
22
                parent1, parent2 = random.sample(selected_population, 2)
23
                child = (parent1 + parent2) / 2
24
            else:
25
                child = random.choice(selected_population)
26

27
            # mutation
28
            if random.random() < mutation_rate:
29
                child += random.uniform(-0.1, 0.1)
30
                # ensure child is within bounds (0, 1)
31
                child = max(0.0001, min(1, child))
32

33
            # add child to new population
34
            new_population.append(child)
35
        population = new_population
36

37
    # return the best solution found in last generation
38
    final_fitness = []
39
    for lambda_val in population:
40
        m, b = lower_opt(x_train, y_train, lambda_val)
41
        eval_fit = upper_eval(x_val, y_val, m, b, lambda_val)
42
        final_fitness.append(eval_fit)
43
    best_lambda = population[np.argmin(final_fitness)]
44
    return best_lambda

run GA for HPO

1
best_lambda = ga_HPO(x_train.reshape(-1, 1), y_train, x_val.reshape(-1, 1), y_val)

final result

1
final_model = Ridge(alpha=best_lambda)
2
final_model.fit(x_train.reshape(-1, 1), y_train)
3

4
# plot results
5
import matplotlib.pyplot as plt
6

7
plt.scatter(x, y, color='blue', label='Data')
8
plt.plot(x, final_model.coef_ * x + final_model.intercept_, color='red', label='Ridge Regression')
9
plt.xlabel('x')
10
plt.ylabel('y')
11
plt.title(f'Ridge Regression with GA-optimized λ: {best_lambda:.4f}')
12
plt.legend()
13
plt.grid()
14
plt.show()