S-curve

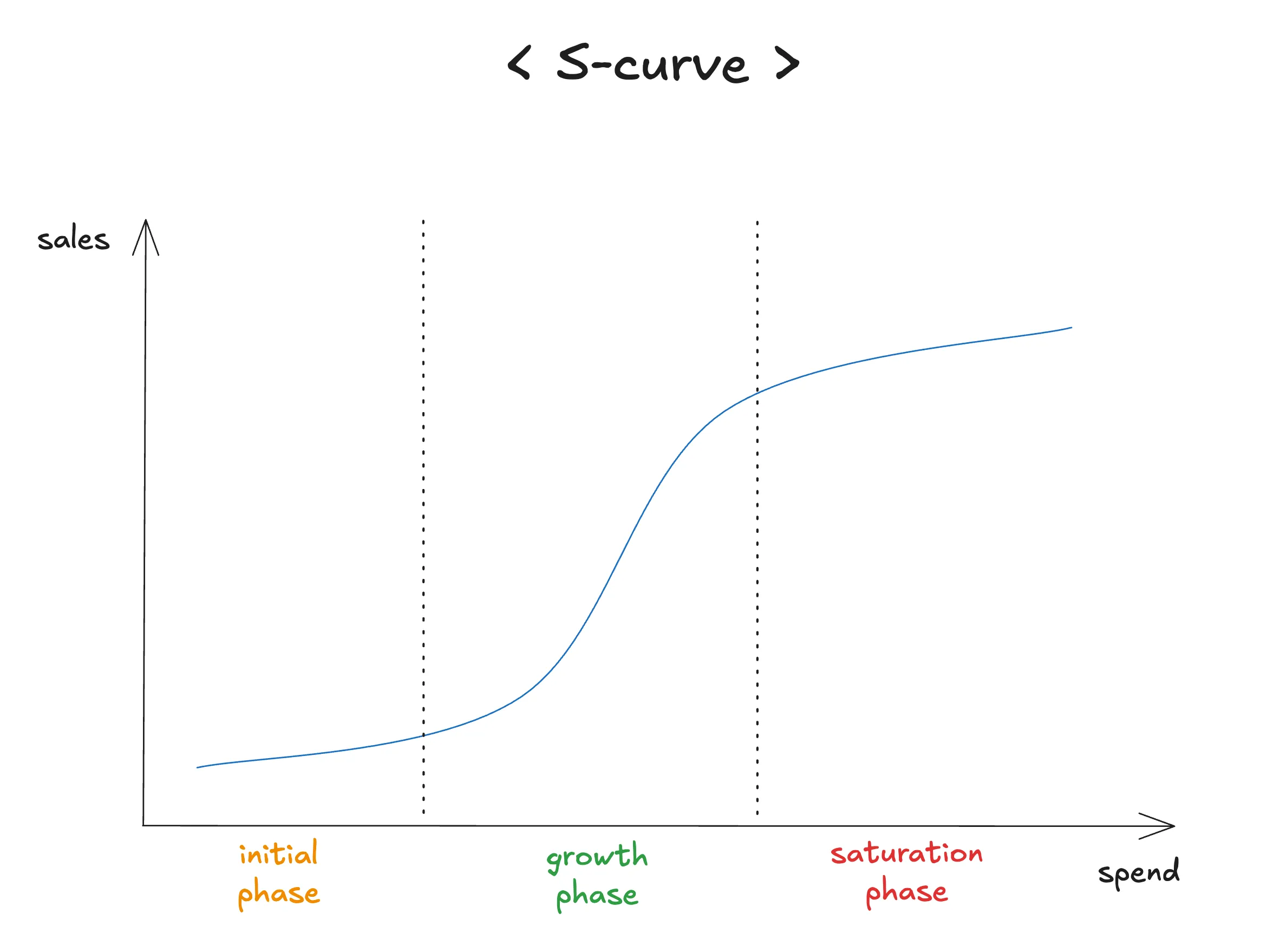
s-curve

S-curve

s-curve

광고비 지출과 그로 인한 성과(매출, 전환 등) 사이의 비선형적(non-linear) 관계를 설명하는 가장 핵심적인 개념. 단순하게 ‘광고비를 2배 쓰면 매출도 2배가 될 것’ 이라는 직선적 가정과 달리, S-Curve는 실제 마케팅 세계에서 나타나는 수익 체감의 법칙(Law of Diminishing Returns) 을 현실적으로 반영. 즉, 광고비 지출이 특정 수준을 넘어서면 효율이 점차 떨어지는 현상을 수학적으로 모델링한 것.

실제 MMM 분석에서는 이러한 S-Curve를 모델링하기 위해 로지스틱 함수(Logistic Function) 나 힐 함수(Hill Function) 와 같은 특정 수학적 함수를 사용하여 통계적으로 곡선을 추정하고 각 채널의 파라미터(곡선의 모양을 결정하는 변수)를 계산.

핵심 구간

점진적 성장 구간 (Ramp-up Phase):

곡선의 위치: S자 곡선의 가장 아랫부분.
특징: 광고비 지출을 시작하는 초기 단계. 아직 시장에 브랜드나 메시지가 충분히 노출되지 않았기 때문에, 광고비를 지출해도 성과가 즉각적이고 비례적으로 나타나지 않습니다. 소비자가 메시지를 인지하고 반응하기까지는 일정 수준의 반복 노출과 시간이 필요.
ROI (투자수익률): 상대적으로 낮음. 이 구간에서는 지출 대비 성과(가성비)가 높지 않게 보일 수 있음.
마케팅 시사점: 최소한의 효과를 보기 위해 넘어야 하는 **‘임계점(Threshold)‘**이 존재하는 구간. 너무 적은 예산을 투입하면 아무런 효과를 보지 못하고 낭비될 수 있음을 의미.

급격한 성장 구간 (Sweet Spot / Steep Growth Phase):

곡선의 위치: S자 곡선의 가운데, 가장 가파른 부분.
특징: 광고 효과가 폭발적으로 증가하는 ‘최적 효율 구간’. 광고 노출이 임계점을 넘어 최적의 빈도에 도달하면서, 적은 추가 비용으로도 가장 큰 성과 증대를 가져옴. 소비자들의 인지도가 급상승하고 구매 전환이 활발하게 일어남.
ROI (투자수익률): 가장 높은 구간입니다. 목표로 해야 할 가장 이상적인 지출 지점(Sweet Spot)이 이 구간에 존재.
마케팅 시사점: 각 미디어 채널별로 이 ‘Sweet Spot’을 찾아내고, 예산을 이 구간에 집중적으로 배분하는 것이 MMM의 핵심 목표.

포화 및 수확 체감 구간 (Saturation / Plateau Phase):

곡선의 위치: S자 곡선의 윗부분, 점점 평평해지는 부분.
특징: 광고비 지출이 일정 수준을 초과하면 시장이 포화상태에 이름. 타겟 고객 대부분에게 이미 메시지가 도달했거나, 소비자들이 광고에 피로감을 느끼기 시작. 이로 인해 광고비를 더 많이 쏟아부어도 성과는 거의 늘지 않거나 아주 미미하게 증가.
ROI (투자수익률): 급격히 감소. 추가적인 지출은 비효율적이며 예산 낭비로 이어질 가능성이 높음.
마케팅 시사점: 특정 채널이 이 구간에 진입했다면, 해당 채널의 예산을 줄이고 아직 포화되지 않은 다른 채널(성장 구간에 있는 채널)로 예산을 재분배하는 전략적 결정이 필요.

S-curve using Logistic Function

\text{Sales} = \frac{A}{1 + e^{-B(\text{Spend} - C)}}

$A$ : 최대 매출 (plateau)
$B$ : 곡선의 기울기 (growth rate)
$C$ : 변곡점 (inflection point)

code implementation example:


5 collapsed lines
1
import numpy as np
2
import pandas as pd
3
import matplotlib.pyplot as plt
4
from scipy.optimize import curve_fit
5

6
# create dataset
7
data = {
8
   'Day' : ['Mon', 'Tue', 'Wed', 'Thu', 'Fri'],
9
   'Spend' : [10, 20, 30, 40, 50],
10
   'Sales' : [200, 250, 400, 450, 460]
11
}
12
df = pd.DataFrame(data)
13

14
# define s-curve function
15
x_data = df['Spend']
16
y_data = df['Sales']
17
def s_curve(x, A, B, C):
18
   return A / (1 + np.exp(-B * (x - C)))
19

20
optimal_params, covariance = curve_fit(
21
   s_curve,
22
   x_data,
23
   y_data,
24
   p0=[max(y_data), 0.1, np.median(x_data)] # initial point (A, B, C)
25
)
26

27
A, B, C = optimal_params
28
print(f"Optimal parameters: A={A}, B={B}, C={C}")
29
# Optimal parameters: A=501.0309931841163, B=0.0844223122026954, C=16.67591505186686
30

31
# plot results
32
x_fit = np.linspace(min(x_data), max(x_data), 100)
33
y_fit = s_curve(x_fit, *optimal_params)
34
plt.scatter(x_data, y_data, label='Data')
35
plt.plot(x_fit, y_fit, color='red', label='Fitted S-Curve')
36
plt.xlabel('Spend')
37
plt.ylabel('Sales')
38
plt.legend()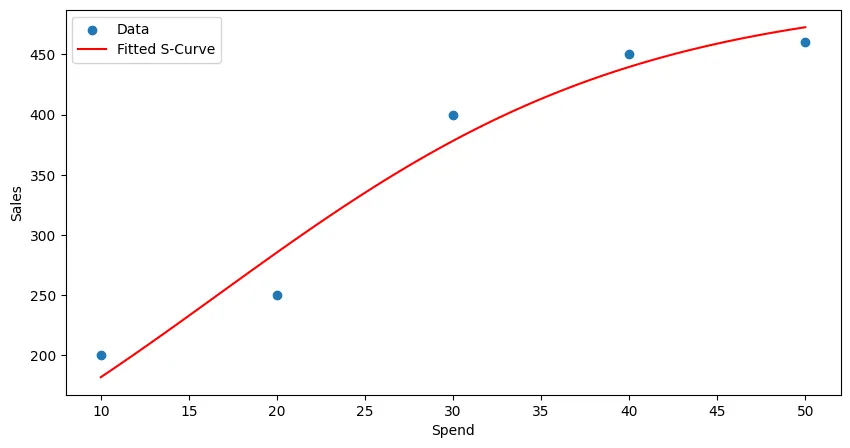

logistic function s-curve-fit

S-curve using generalized logistic function (Richards’ curve)

\text{Sales} = A(1+ve^{-B(\text{Spend}-C)})^{-\frac{1}{v}}

$A$ : 최대 매출 (plateau)
$B$ : 곡선의 기울기 (growth rate)
$C$ : 변곡점 (inflection point)
$v$ : 곡선의 비대칭성 조절 (asymmetry parameter)

if $v=1$ , 일반적인 로지스틱 함수와 동일.
if $v<1$ , 초기에 완만하게 증가하다가 급격히 증가하는 형태. (slow early growth, rapid later growth)
if $v>1$ , 초기에 급격히 증가하다가 완만하게 증가하는 형태. (rapid early growth, slow later growth)

code implementation example:


5 collapsed lines
1
import numpy as np
2
import pandas as pd
3
import matplotlib.pyplot as plt
4
from scipy.optimize import curve_fit
5

6
# create dataset
7
data = {
8
   'Day' : ['Mon', 'Tue', 'Wed', 'Thu', 'Fri'],
9
   'Spend' : [10, 20, 30, 40, 50],
10
   'Sales' : [200, 250, 400, 450, 460]
11
}
12
df = pd.DataFrame(data)
13

14
# define s-curve function
15
x_data = df['Spend']
16
y_data = df['Sales']
17
def s_curve(x, A, B, C, nu=1):
18
   return A * (1 + nu*np.exp(-B * (x - C)))**(-1/nu)
19

20
optimal_params, covariance = curve_fit(
21
   s_curve,
22
   x_data,
23
   y_data,
24
   p0=[max(y_data), 0.1, np.median(x_data), 0.9] # initial point (A, B, C, nu)
25
)
26

27
A, B, C, nu = optimal_params
28
print(f"Optimal parameters: A={A}, B={B}, C={C}, nu={nu}")
29
# Optimal parameters: A=455.0000003735234, B=4.078058186448524, C=32.74072510361706, nu=108.54222404122513
30

31
# plot results
32
x_fit = np.linspace(min(x_data), max(x_data), 100)
33
y_fit = s_curve(x_fit, *optimal_params)
34
plt.scatter(x_data, y_data, label='Data')
35
plt.plot(x_fit, y_fit, color='red', label='Fitted S-Curve')
36
plt.xlabel('Spend')
37
plt.ylabel('Sales')
38
plt.legend()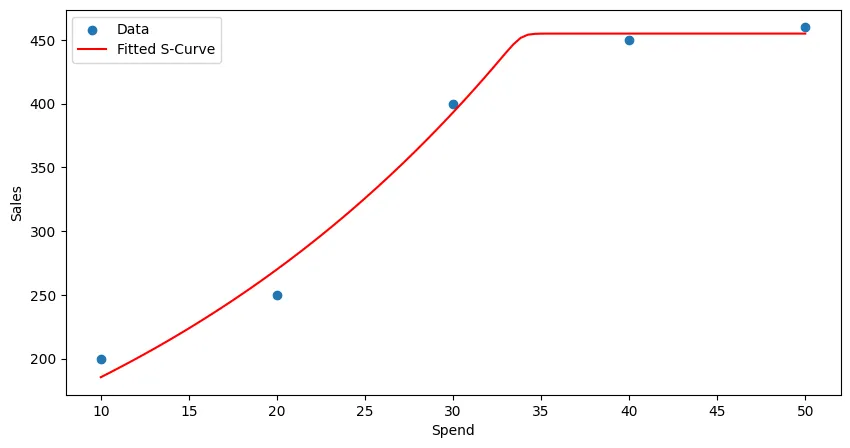

generalizedlogistic function s-curve-fit

S-curve using Hill Function

\text{Sales} = \frac{A \cdot \text{Spend}^n}{K^n + \text{Spend}^n}

$A$ : 최대 매출 (plateau)
$K$ : 반응의 절반이 최대에 도달하는 지출 수준 (half-maximal point)
$n$ : 곡선의 기울기 (growth rate)