Overview

budget allocation practice using variable transformation

hyungjun hyungjun
September 9, 2025
6 min read
machine learning ai adtech mmm mdmm
practice

Problem Statement

  1. Load data: dt_simulated_weekly.csv

  2. Randomly select a hyperparameter set and do the adstock and saturation transformation

  3. Fit the MMM model (single objective)

    • Use the transformed variables.
    • Assume a simple linear model, y=intercept+β1⋅f1(media_variable1)+⋯+βn⋅fn(media_variablen)y = \text{intercept} + \beta_1 \cdot f_1(\text{media\_variable}_1) + \cdots + \beta_n \cdot f_n(\text{media\_variable}_n)

  4. Find the optimal budget allocation with an initial spend of $20,000 for each media.

Solution

Load Data

# import libraries and set seed
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from scipy.optimize import minimize
np.random.seed(42)
  • data 조작을 위해 pandas, numpy 사용.
  • Task 에서 선형 모델을 가정하라고 하였기에 sklearn 의 LinearRegression 을 사용.
  • 최적화 문제 해결을 위해 scipy.optimize 의 minimize 사용.
  • 시각화를 위해 matplotlib.pyplot 사용.
  • 재현성을 위해 시드 고정.
# load data
df = pd.read_csv('dt_simulated_weekly-1.csv')
df.head()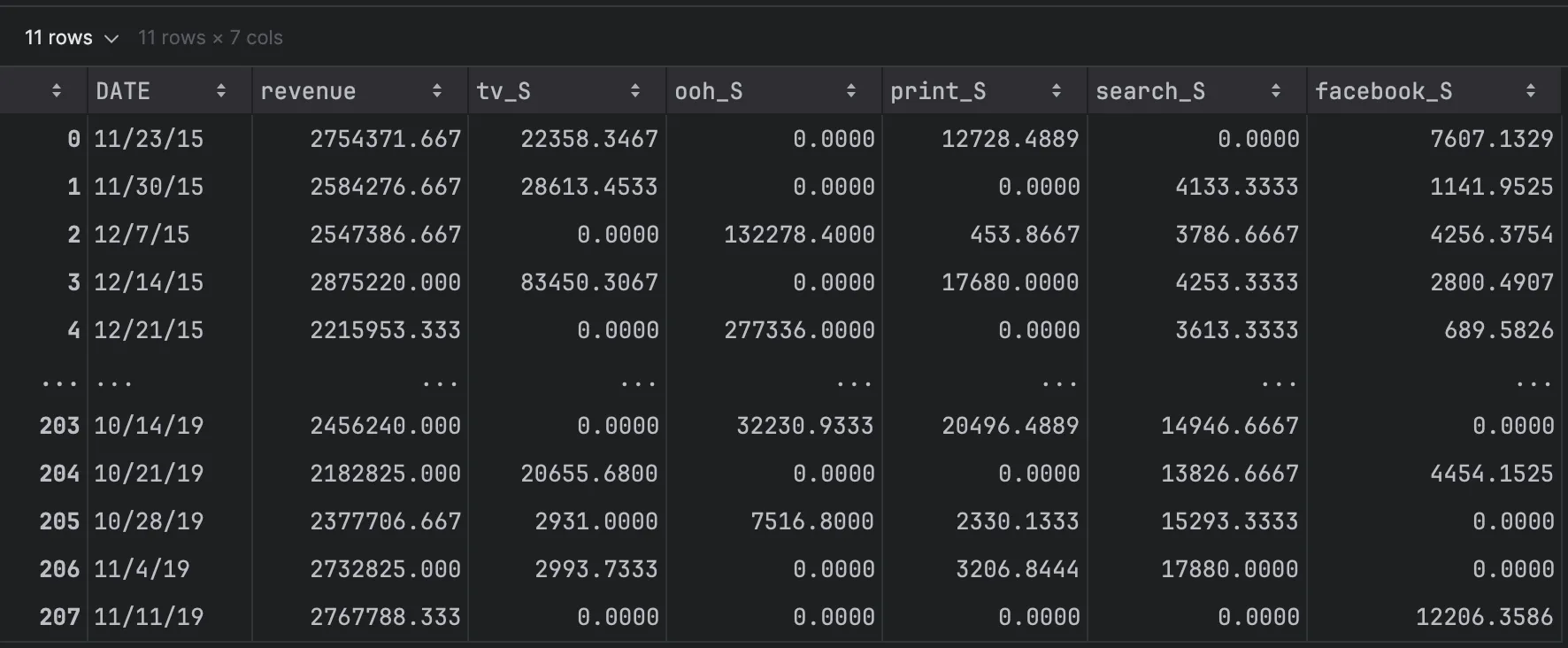

practice-data

  • 데이터는 주 단위로 수집된 시계열 데이터임을 확인할 수 있음.
  • 각 컬럼의 의미는 다음과 같음:
    • DATE: 주 단위 시간 정보
    • revenue: 매출 (종속 변수)
    • tv_S, ooh_S, print_S, search_S, facebook_S: 광고 채널별 지출 (독립 변수)

결측치의 경우 없음을 확인하였으며, 실제 데이터에서는 결측치 처리 및 이상치 탐지 등의 전처리 과정이 필요할 수 있음.

Variable Transformation

# define media channels
media_channels = ['tv_S', 'ooh_S', 'print_S', 'search_S', 'facebook_S']


# define geometric adstock function
def geometric_adstock(spend_series, decay_rate):
    adstocked_spend = np.zeros_like(spend_series, dtype=float)
    adstocked_spend[0] = spend_series[0]
    for i in range(1, len(spend_series)):
        adstocked_spend[i] = spend_series[i] + decay_rate * adstocked_spend[i-1]
    return adstocked_spend


# define hill saturation function
def hill_saturation(adstocked_spend, alpha, gamma):
    epsilon = 1e-9 # prevent division by zero
    return 1 / (1 + ((gamma + epsilon)/adstocked_spend)**(alpha))


# set hyperparameters using random values within reasonable ranges
df_transformed = df.copy()
hyperparameters = {}


for channel in media_channels:
    decay_rate = np.random.uniform(0.1, 0.9)
    alpha = np.random.uniform(1.0, 5.0)
    gamma = np.random.uniform(0.1, 1.0) * df[channel].mean()


    # add hyper parameters for each channel
    hyperparameters[channel] = {'decay_rate': decay_rate, 'alpha': alpha, 'gamma': gamma}


    # apply adstock / saturation transformations
    adstocked_spend = geometric_adstock(df[channel], decay_rate)
    saturated_spend = hill_saturation(adstocked_spend, alpha, gamma)
    df_transformed[f'{channel}_adstocked'] = adstocked_spend
    df_transformed[f'{channel}_saturated'] = saturated_spend


# check transformed data in dataframe
df_transformed.head()
  • parent document 에서 언급한 geometric adstock transformation 과 hill saturation transformation 을 각각 함수로 정의.
  • 각 광고 채널별로 decay rate, alpha, gamma 의 hyperparameter 를 랜덤하게 설정하여 변환을 수행.
    • 각 변수의 범위 제한을 고려.
    • saturation 의 gamma 의 경우 채널별 평균 지출의 10% ~ 100% 사이로 설정.
  • transformed variables 는 각각 _adstocked, _saturated suffix 를 붙여서 dataframe 에 추가.
Note (reference)

Randomly Selected Hyperparameters:

media channel: tv_S
  - Adstock Decay Rate (theta): 0.3996
  - Saturation Alpha (shape): 4.8029
  - Saturation Gamma (scale): 11263.3120


media channel: ooh_S
  - Adstock Decay Rate (theta): 0.5789
  - Saturation Alpha (shape): 1.6241
  - Saturation Gamma (scale): 10389.3799


media channel: print_S
  - Adstock Decay Rate (theta): 0.1465
  - Saturation Alpha (shape): 4.4647
  - Saturation Gamma (scale): 2390.0664


media channel: search_S
  - Adstock Decay Rate (theta): 0.6665
  - Saturation Alpha (shape): 1.0823
  - Saturation Gamma (scale): 5755.3140


media channel: facebook_S
  - Adstock Decay Rate (theta): 0.7660
  - Saturation Alpha (shape): 1.8494
  - Saturation Gamma (scale): 565.6865

Saturation Curves:

saturation-curves

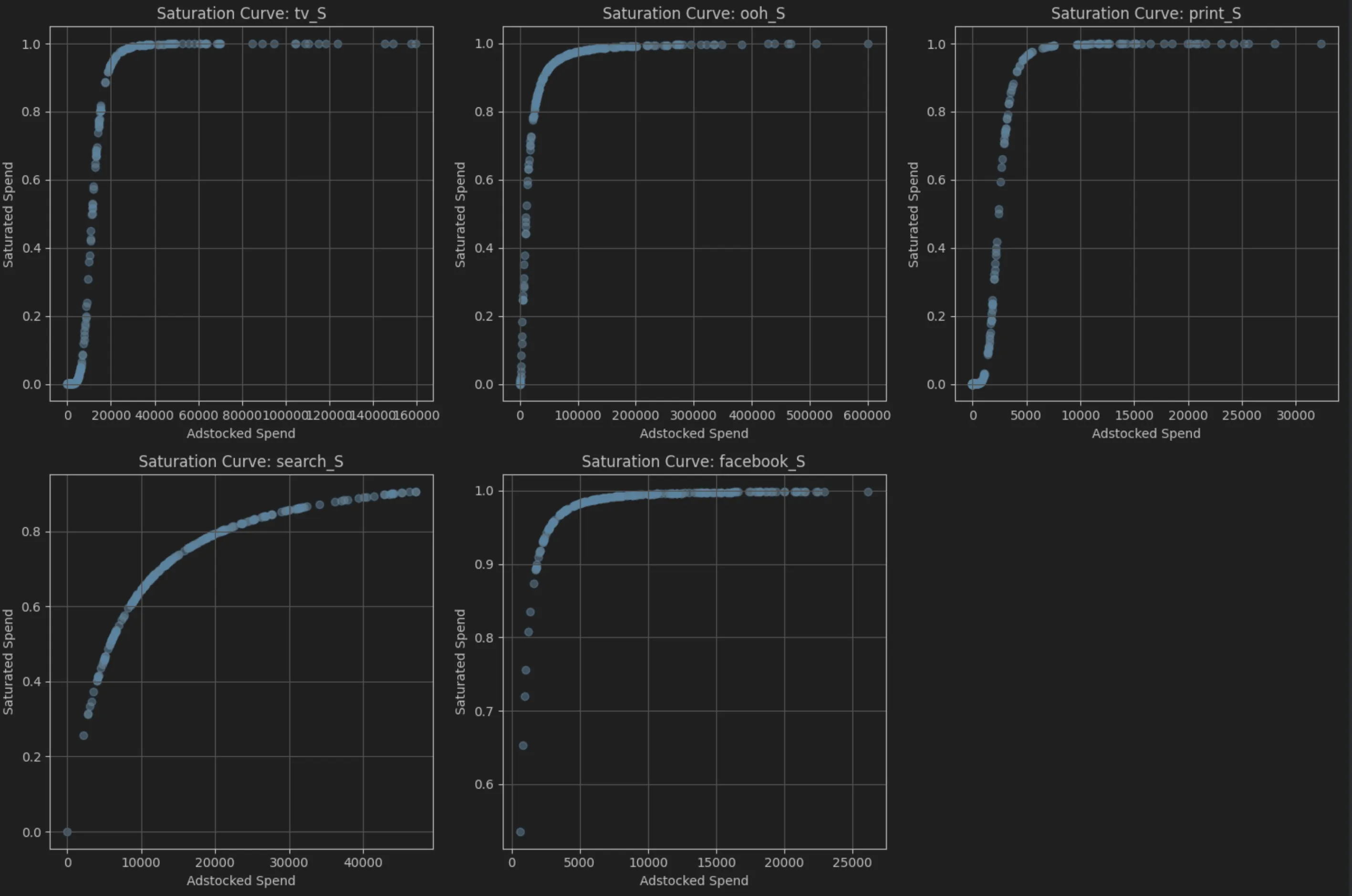
saturation 의 경우 “the law of diminishing returns” 를 반영하기에 adstock spend를 x축으로, saturated spend를 y축으로 하여 그리면 S-curve 형태가 됨을 시각적으로 확인할 수 있음.

Fit MdMM model using linear regression

# prepare X and y
X = df_transformed[[f'{c}_saturated' for c in media_channels]]
y = df_transformed['revenue']


# create and train linear regression model
model = LinearRegression()
model.fit(X, y)
r_squared = model.score(X, y)
  • Task 에서 제시한 선형 모델을 가정하여 saturated 변수들로 독립변수 행렬 X 를 구성.
  • 종속변수 y 는 revenue 로 설정.
  • R-squared 값을 통해 모델의 설명력을 평가 → 0.4927 (선형 모델로는 설명력이 다소 낮음을 확인할 수 있음)

Budget Allocation Optimization

budget allocation 의 경우 두 가지 접근법이 가능함:

  1. 과거 데이터의 바로 이후 기간에 대한 예산 할당을 최적화하는 접근 → 직전 데이터의 adstock_spend 를 고려 필요.
  2. adstock 효과를 무시하고 단순히 지출에 대한 saturation 효과만 고려하는 접근

1번 접근법:

# define revenue prediction functions for optimization
def predict_revenue_with_consider_adstock_spend(spends, channels, h_params, intercept, coefs):
    transformed_spends = []
    for i, channel in enumerate(channels):
        spend = spends[i]
        alpha = h_params[channel]['alpha']
        gamma = h_params[channel]['gamma']


        # use last date's adstocked spend * decay rate + current spend as adstocked spend
        # this assumes that we are right after the last date in the dataset and the adstock effect is still ongoing
        adstocked_spend = df_transformed[f'{channel}_adstocked'].iloc[-1] * h_params[channel]['decay_rate'] + spend
        saturated_spend = hill_saturation(adstocked_spend, alpha, gamma)
        transformed_spends.append(saturated_spend)


    predicted_revenue = intercept + np.dot(transformed_spends, coefs)


    # convert maximization problem to minimization
    return -predicted_revenue
  • 마지막 과거 데이터 (208 인덱스)의 adstocked 값을 고려하여 바로 다음 주의 지출을 최적화.
  • adstocked 값은 decay rate 를 곱하여 감소시킨 후, 현재 지출을 더하여 계산.
  • saturated 값은 앞서 정의한 hill_saturation 함수를 사용하여 계산.

최적화를 위해 maximization 문제를 minimization 문제로 변환.

2번 접근법:

def predict_revenue_ignore_last_adstock_spend(spends, channels, h_params, intercept, coefs):
    transformed_spends = []
    for i, channel in enumerate(channels):
        spend = spends[i]
        alpha = h_params[channel]['alpha']
        gamma = h_params[channel]['gamma']


        # ignore last adstocked spend, just use current spend as adstocked spend
        # this assumes that the adstock effect has completely decayed by the time we are making the prediction
        saturated_spend = hill_saturation(spend, alpha, gamma)
        transformed_spends.append(saturated_spend)


    predicted_revenue = intercept + np.dot(transformed_spends, coefs)
    return -predicted_revenue
  • adstock 효과를 무시하고 현재 지출만을 고려하여 saturated 값을 계산.
  • 이는 adstock 효과가 완전히 사라졌다고 가정하는 접근법.

Optimize Budget Allocation

1번 접근법:

# parameters for optimization
initial_spends = [20000] * len(media_channels) # $20,000 per channel
total_budget = sum(initial_spends) # $100,000
constraints = ({'type': 'eq', 'fun': lambda spends: total_budget - np.sum(spends)}) # total budget constraint
bounds = [(0, total_budget) for _ in media_channels] # non-negative spends
model_coefs = model.coef_ # get model coefficients


# perform optimizaton
result_consider_last_adstock_spend = minimize(
    fun=predict_revenue_with_consider_adstock_spend,
    x0=initial_spends,
    args=(media_channels, hyperparameters, model.intercept_, model_coefs),
    method='SLSQP', # bcs we have constraints
    bounds=bounds,
    constraints=constraints
)


# print optimization results for both methods
if result_consider_last_adstock_spend.success:
    optimal_spends = result_consider_last_adstock_spend.x
    max_revenue = -result_consider_last_adstock_spend.fun


    print("--- Budget Optimization Results considering Last Adstocked Spend ---")
    print(f"\nTotal Budget: ${total_budget:,.2f}")


    allocation_df = pd.DataFrame({
        'Channel': media_channels,
        'Optimal Spend': optimal_spends
    })
    allocation_df['Percentage'] = (allocation_df['Optimal Spend'] / total_budget) * 100
    print("\nOptimal Budget Allocation:")
    print(allocation_df.to_string(index=False, formatters={'Optimal Spend': '${:,.2f}'.format, 'Percentage': '{:.2f}%'.format}))


    initial_predicted_revenue = -predict_revenue_with_consider_adstock_spend(initial_spends, media_channels, hyperparameters, model.intercept_, model_coefs)


    print(f"\nExpected Maximum Revenue after Optimization: ${max_revenue:,.2f}")
    print(f"Expected Revenue with Equal Distribution: ${initial_predicted_revenue:,.2f}")
    print(f"Expected Revenue Uplift: ${max_revenue - initial_predicted_revenue:,.2f} ({(max_revenue/initial_predicted_revenue - 1)*100:.2f}%)")

2번 접근법:

result_ignore_last_adstock_spend = minimize(
    fun=predict_revenue_ignore_last_adstock_spend,
    x0=initial_spends,
    args=(media_channels, hyperparameters, model.intercept_, model_coefs),
    method='SLSQP', # bcs we have constraints
    bounds=bounds,
    constraints=constraints
)


if result_ignore_last_adstock_spend.success:
    optimal_spends_ignore = result_ignore_last_adstock_spend.x
    max_revenue_ignore = -result_ignore_last_adstock_spend.fun


    print("\n--- Budget Optimization Results ignoring Last Adstocked Spend ---")
    print(f"\nTotal Budget: ${total_budget:,.2f}")


    allocation_df_ignore = pd.DataFrame({
        'Channel': media_channels,
        'Optimal Spend': optimal_spends_ignore
    })
    allocation_df_ignore['Percentage'] = (allocation_df_ignore['Optimal Spend'] / total_budget) * 100
    print("\nOptimal Budget Allocation:")
    print(allocation_df_ignore.to_string(index=False, formatters={'Optimal Spend': '${:,.2f}'.format, 'Percentage': '{:.2f}%'.format}))


    initial_predicted_revenue_ignore = -predict_revenue_ignore_last_adstock_spend(initial_spends, media_channels, hyperparameters, model.intercept_, model_coefs)


    print(f"\nExpected Maximum Revenue after Optimization: ${max_revenue_ignore:,.2f}")
    print(f"Expected Revenue with Equal Distribution: ${initial_predicted_revenue_ignore:,.2f}")
    print(f"Expected Revenue Uplift: ${max_revenue_ignore - initial_predicted_revenue_ignore:,.2f} ({(max_revenue_ignore/initial_predicted_revenue_ignore - 1)*100:.2f}%)")

각 접근법의 결과는 다음과 같음:

--- Budget Optimization Results considering Last Adstocked Spend --- (1st approach)


Total Budget: $100,000.00


Optimal Budget Allocation:
   Channel Optimal Spend Percentage
      tv_S    $25,608.69     25.61%
     ooh_S    $35,313.57     35.31%
   print_S     $5,851.00      5.85%
  search_S    $33,226.74     33.23%
facebook_S         $0.00      0.00%


Expected Maximum Revenue after Optimization: $2,640,643.02
Expected Revenue with Equal Distribution: $2,541,850.71
Expected Revenue Uplift: $98,792.30 (3.89%)


--- Budget Optimization Results ignoring Last Adstocked Spend --- (2nd approach)


Total Budget: $100,000.00


Optimal Budget Allocation:
   Channel Optimal Spend Percentage
      tv_S    $23,459.44     23.46%
     ooh_S    $27,002.46     27.00%
   print_S     $5,118.77      5.12%
  search_S    $36,701.82     36.70%
facebook_S     $7,717.51      7.72%


Expected Maximum Revenue after Optimization: $2,527,572.87
Expected Revenue with Equal Distribution: $2,362,181.37
Expected Revenue Uplift: $165,391.49 (7.00%)
  • 두 접근법 모두 예산을 최적화하여 매출을 증가시킴을 확인할 수 있음.
  • 1번 접근법의 경우가 adstock 효과과 고려되어 총 매출이 더 높게 나타남을 확인할 수 있음.